Selection Sort and Big O Notation
Checkpoint #3
public class SelectionSort {
public int comparisons = 0; // creates primitive data types
public int swaps = 0; // public so it's used by both methods
public static void main(String[] args) { // main method
long start = 0; // initializes long which is a primitive data type that stores whole numbers. common type of initialization for a counter or timer that needs to be incremented or decremented as part of a program's logic
long end = 0;
// create a new SelectionSort object
SelectionSort selectionSort = new SelectionSort();
for (int i=0;i<12;i++) { // create 12 arrays as per requirements
// generate 5000 random elements
int[] array = new int[5000]; // creates a new array with 5000 integer
for (int j=0;j<5000;j++) {
array[j] = (int)(Math.random()*10000);
} // for loop generates the elements using random (math.random is only 0-1 so you mulitiply by 10000 to get bigger number)
// sort the array
start += System.currentTimeMillis(); // before you start the sorting, it stores the current time
selectionSort.sort(array); // sorts
end += System.currentTimeMillis(); // stores the end time
}
// get average
System.out.println("Average time taken: " + (end-start)/12 + " ms");
System.out.println("Average comparisons: " + selectionSort.comparisons/12);
System.out.println("Average swaps: " + selectionSort.swaps/12);
}
public void sort(int[] numbers) { // selection sort algorithm
int n = numbers.length; // figures out the length of the array
for (int i = 0; i < n - 1; i++) { // for loop used to repeatedly finds the minimum value and swaps it
int minIndex = i; // outer loop iterates through array numbers and the minimum value is set to i
for (int j = i + 1; j < n; j++) { // The inner loop iterates through unsorted portion of the array after the current index i to the last element the algorithm compares the current element with the minimum element found so far
comparisons++; // records the number of comparision
if (numbers[j] < numbers[minIndex]) { // inside loop checks if the index is different from the current value
minIndex = j; // if it is, the current value is set as the index
}
}
if (minIndex != i) { // stores value of first element in the temp variable and then copying the value of the temporary variable to the minimum element's original position
int temp = numbers[i];
numbers[i] = numbers[minIndex];
numbers[minIndex] = temp;
swaps++; // number of swaps is implementing
}
}
System.out.println("Comparisons: " + comparisons);
System.out.println("Swaps: " + swaps);
}
}
SelectionSort.main(null);
Evaluation of Sorts
- Selection Sort: 20 ms
- Insertion Sort: 6 ms
- Merge Sort: 14 ms
- Bubble Sort: 22 ms
- Insertion Sort is the fastest at 6 ms which is weird because it also had the highest number of comparision and swaps. It should've been the lowest number of comparision and swaps since those take time.
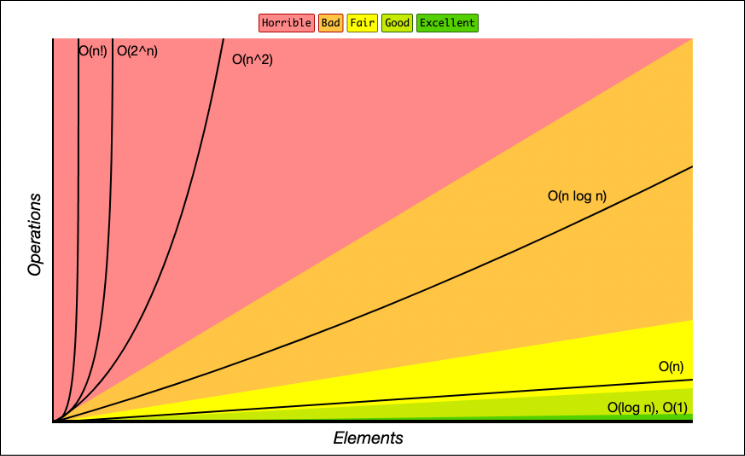
Big O Notation Notes
- simplified analysis of an algorithm's efficiency
- gives complexity based on input size, n
- analyze time and space complexity
- types of measurements for effiecieny: worst case, best case, and average case
- Big O notation typically looks at worst case
- Rules: ignore constants, ceratin terms dominate others
- Constant time: x = 5 +(15*20) is not dependent on size so the big O notation is O(1)
- Linear time: O(N)
import java.util.HashMap;
import java.util.Random;
public class ExampleHashMapSearch {
public static void main(String[] args) {
// Create a new HashMap object with 5000 elements
HashMap<Integer, String> myHashMap = new HashMap<>();
for (int i = 0; i < 5000; i++) {
myHashMap.put(i, "value_" + i);
}
// Perform 12 searches with random keys
int numSearches = 12; // search for 12 different elements
int numKeys = 100;
int[] searchTimes = new int[numSearches];
Random rand = new Random();
for (int i = 0; i < numSearches; i++) {
// Generate random keys to search for
int[] keys = new int[numKeys];
for (int j = 0; j < numKeys; j++) {
keys[j] = rand.nextInt(5000);
}
// Search for the keys and record the time taken
long startTime = System.nanoTime();
for (int j = 0; j < numKeys; j++) {
myHashMap.get(keys[j]);
}
long endTime = System.nanoTime();
searchTimes[i] = (int) ((endTime - startTime)); // Convert nanoseconds to milliseconds
}
// Calculate the average search time
int sum = 0;
for (int i = 0; i < numSearches; i++) {
sum += searchTimes[i];
}
int avg = sum / numSearches;
// Print the results
System.out.println("Average search time: " + avg + " nanoseconds");
}
}
ExampleHashMapSearch.main(null);
Extra
- Compare pros and cons of collections
| Name | Pros | Cons |
|---|---|---|
| Collections | Framework for storing and manipulating groups of objects, flexible and useful for different data types and structures, easy to add search delete elements, easy to iterate through. | Not efficient for large datasets, no fast random access to elements. |
| Hashmaps | fast way to look up values by key, hash tables are efficient for large datasets. | Don't maintain order of elements, more memory, slower iteration than arrays or simple lists. |